This is the multi-page printable view of this section. Click here to print.
Misc
- 1:
- 2: Graphviz: Spline-o-Matic
- 3: Sql2Dot
1 -
2 - Graphviz: Spline-o-Matic
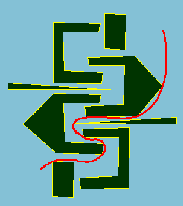
Spline-o-matic is an edge router that draws Bezier curves in diagrams. It comes with a TCL/tk interface for tests and demos.
The library accepts as input:
-
two endpoints
-
optional endpoint tangent vectors
-
an admissible region where a curve may be drawn to connect the endpoints
It returns a Bezier curve that connects the endpoints and stays within the admissible region. The curve is smooth and close to a shortest path.
Spline-o-matic Solves Two Types of Problems
In the first case, the input is a simple polygon, with the two endpoints must be inside it. The result curve stays within the control polygon.
In the second case, the input is a list of polygonal obstacles or "holes" to be avoided, along with the endpoints. The result curve does not pass through any obstacle . (If an endpoint is inside an obstacle, it is ignored for the given route. This is convenient for routing node-link diagrams.)
Curves are routed individually, not globally, so the edge router does not prevent them from crossing. An interesting improvement to this library would be introduce some notion of global planning to prevent unwanted edge crossings. The library interface to Spline-o-matic exposes its main algorithms so they may be invoked independently for efficiency and flexibility.
Curves are computed in two phases. The first phase finds a shortest path (a polyline) between endpoints. As described previously, there are two variants. Routing inside a polygon is solved by an efficient algorithm due to Overmars and Welzl, but routing around obstacles involves computing the visibility graph of the obstacles' vertices, for which we employ the standard O(N^3) algorithm. When more than one edge route is to be found, it is much faster to precompute and re-use the visibility graph, than to compute it for each route.
The second phase takes an arbitrary simple path (usually a shortest path computed by the first phase) and a list of barrier segments (usually sides of a control polygon or of obstacles) and produces a Bezier curve that does not touch a barrier except on an endpoint. Note that the barriers are not required to form polygons.
Here is the library API. Polygons must always be presented in clockwise order!
#include <pathgeom.h>
/* open a visibility graph */
vconfig_t *Pobsopen(Ppoly_t **obstacles, int n_obstacles);
/* close a visibility graph, freeing its storage */
void Pobsclose(vconfig_t *config);
/* route a polyline from p0 to p1, avoiding obstacles.
* if an endpoint is inside an obstacle, pass the polygon's index >=0
* if the endpoint is not inside an obstacle, pass POLYID_NONE
* if the endpoint location is not known, pass POLYID_UNKNOWN
*/
int Pobspath(vconfig_t *config, Ppoint_t p0, int poly0,
Ppoint_t p1, int poly1,
Ppolyline_t *output_route);
#define POLYID_NONE -1111
#define POLYID_UNKNOWN -2222
/* find shortest euclidean path within a simple polygon */
extern int Pshortestpath(Ppoly_t *boundary, Ppoint_t endpoints[2],
Ppolyline_t *output_route);
/* fit a spline to an input polyline, without touching barrier segments */
extern int Proutespline (Pedge_t *barriers, int n_barriers,
Ppolyline_t input_route, Pvector_t endpoint_slopes[2],
Ppolyline_t *output_route);
/* utility function to convert from a set of polygonal obstacles to barriers */
extern int Ppolybarriers(Ppoly_t **polys, int npolys, Pedge_t **barriers, int *n
_barriers);
#endif
Distribution
The source release is on our download page. Considerable software know-how is needed to work with it. The GUI is written in TCL. The path planner is built as a static library. The TCL layer includes this and other functions as a dynamic library.
GUI
The package has a C library interface and a TCL/tk GUI (contributed
by John Ellson, ellson@research.att.com) for demos and debugging.
Run pathtest.tcl (or tclsh pathtest.tcl). The GUI permits drawing
obstacle polygons (use button 1 to place vertices and button 2 to
place the last vertex of a polygon).
pathtest comes with a few
sample obstacle configurations.
To try it, run pathtest.tcl.
load an example, click on the Bezier radio button,
and use mouse button 1 and 2 to sweep a line segment.
A curve will be routed between its endpoints.
The choice of routing inside a polygon or routing around
obstacles depends on the endpoints.
References
Implementing a General-purpose Edge Router: Paper, Quicktime video.
3 - Sql2Dot
Sql2Dot is a tiny parser written in java to transform sql into dot for visualizing data structures. It parses some very basic sql which we use in PostgreSQL. Here is an example of sql (borrowed from lain) that Sql2Dot likes to parse.
Source and class files can be found in this sql2dot.jar file
Usage: java -jar sql2dot.jar <files>
<files> - list of sql files
Sql2Dot sends its output to the same location and name as the specified file with a '.dot' on the end.
Example:
Let's say we have a file with sql commands for creating tables called 'foo.sql'
We parse it like this: java -jar sql2dot.jar foo.sql
That will create foo.sql.dot
We can then run this file through dot to create a PNG
dot -Tpng foo.sql.dot -o foo.png
It would be nice if someone would throw a real sql parser on it ;)
The source is public domain. Do with it as you see fit. It would be nice to see improvements make their way back here :)
DISCLAIMER: I'm not resposbile for the software's or your actions.
Enjoy!
Robert Dale <rdale@digital-mission.com>